Project Overview
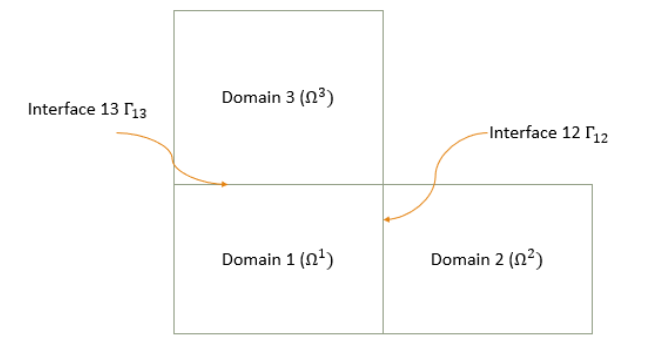
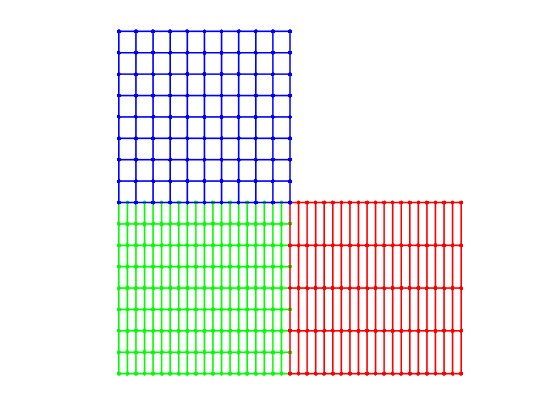
This project explores the application of Nitsche's Method in Finite Element Analysis (FEA) to address challenges in multi-patch geometries with non-conforming meshes. Nitsche's formulation adds interface terms to enforce continuity and boundary conditions while preserving stability and accuracy, even across disconnected mesh patches.
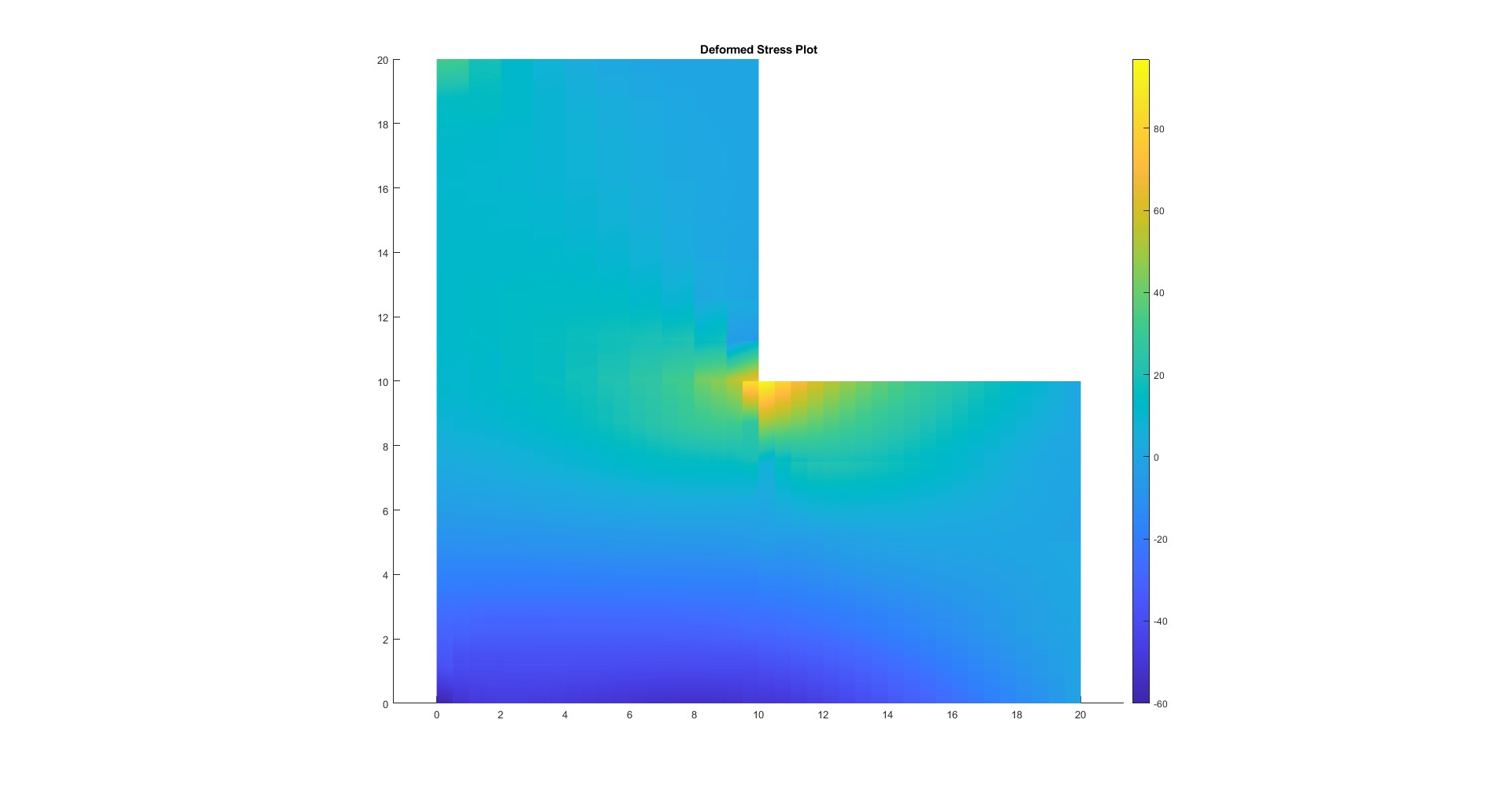
The approach is particularly powerful in problems involving linear elasticity and complex geometrical domains. Key mathematical operators such as the jump and average are implemented to bridge mesh gaps. This project demonstrates how Nitsche's Method enables high-fidelity solutions in computational mechanics where standard FEA would otherwise struggle.
Visual Results
1. L-shaped Geometry
2. Meshing of the Geometry
3. Loading and Boundary Conditions
4. Displacement Plot
5. Stress Plot
6. Stress Plot from -30 to 30 to Observe Solution Continuity
Tools Used: MATLAB
Category: Computational Mechanics, Structural FEA, Advanced FEM Techniques